Denoising Diffusion Probabilistic Models (DDPM) 阅读笔记

给定初始数据分布 \(x_0 \sim q(x)\)，可以不断地向分布中添加高斯噪声。该噪声的标准差由固定值 \(\beta_t\) 确定，均值由固定值 \(\beta_t\) 和当前时刻 \(t\) 的数据 \(x_t\) 决定。此过程是一个马尔可夫链过程。
随着 \(t\) 的不断增大，最终数据分布 \(x_T\) 会逐渐变为一个各向同性的高斯分布（各向独立的高斯分布）。

前向过程

参数解释重要性质

\(x_0\): 原始数据（如图像）
\(x_t\): 第t步的噪声数据
\(\beta_t\): 噪声调度参数，控制每一步添加的噪声量
\(\mathcal{N}\): 高斯分布
\(I\): 单位矩阵

任意时刻t的分布可以直接计算(采用了重参数化的技巧)：\(q(x_t|x_0) = \mathcal{N}(x_t; \sqrt{\bar{\alpha}_t}x_0, (1-\bar{\alpha}_t)I)\) 其中 \(\alpha_t = 1-\beta_t\), \(\bar{\alpha}_t = \prod_{s=1}^t \alpha_s\)

数学推导详解

前向过程重参数化后验概率计算均值预测简化

前向过程的关键是可以重参数化为：

\[x_t = \sqrt{\bar{\alpha}_t}x_0 + \sqrt{1-\bar{\alpha}_t}\epsilon\]

其中\(\epsilon \sim \mathcal{N}(0, I)\)是标准高斯噪声。

这种表示方式使得我们可以在任意时间步t直接从\(x_0\)采样\(x_t\)，无需逐步添加噪声。

通过贝叶斯定理和马尔可夫链性质，可以推导出：

\[q(x_{t-1}|x_t, x_0) = \mathcal{N}(x_{t-1}; \tilde{\mu}_t(x_t, x_0), \tilde{\beta}_t I)\]

其中：

\(\tilde{\mu}_t(x_t, x_0) = \frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1-\bar{\alpha}_t}x_0 + \frac{\sqrt{\alpha_t}(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t}x_t\)
\(\tilde{\beta}_t = \frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t}\beta_t\)

通过进一步推导，上述均值可以重写为：

\[\tilde{\mu}_t(x_t, x_0) = \frac{1}{\sqrt{\alpha_t}}\left(x_t - \frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\epsilon_t\right)\]

其中\(\epsilon_t\)是添加到\(x_0\)的噪声。这表明我们可以通过预测噪声\(\epsilon_t\)来生成逆向过程。

反向过程详解

反向过程（去噪过程）

逆过程是从高斯噪声中恢复原始数据，我们可以假设它也是一个高斯分布，但是无法逐步地去拟合分布，所以需要构建一个参数分布来去做估计。逆扩散过程仍然是一个马尔科夫链过程。

逆扩散过程

参数解释关键发现

\(\theta\): 神经网络参数
\(\mu_\theta\): 神经网络预测的均值
\(\Sigma_\theta\): 神经网络预测的方差
\(p(x_T)\): 标准高斯分布

预测噪声比预测均值效果更好
方差可以固定为\(\beta_t\)或\(\tilde{\beta}_t\)
使用简化的训练目标可以获得更好的样本质量

训练目标详解

目标数据分布的似然函数

在负对数似然函数的基础上加上一个KL散度项，就构成了负对数似然函数的上界，上界越小，负对数似然函数越小，对数似然函数就越大。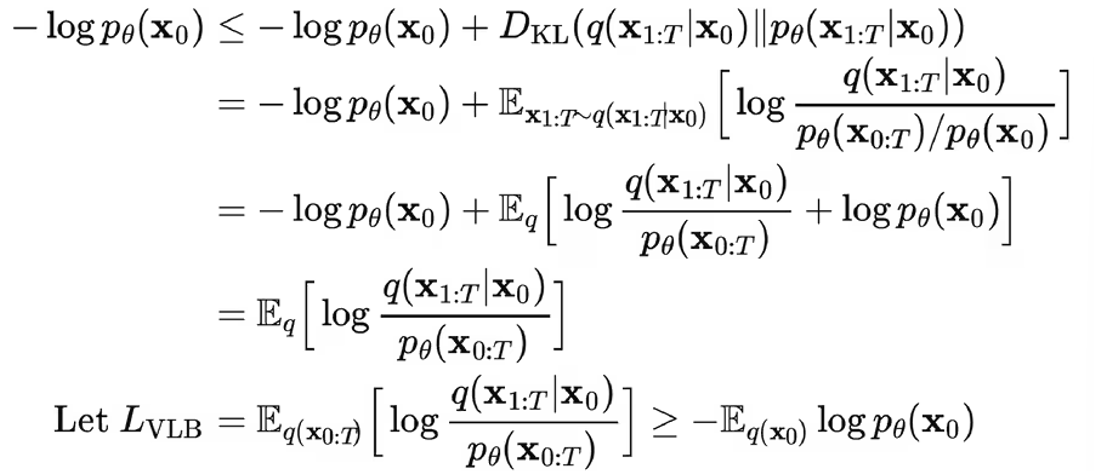目标数据分布的似然函数进一步可以写出交叉熵的上界，并对交叉熵的上界进行化简：

ELBO的重写形式简化训练目标训练算法

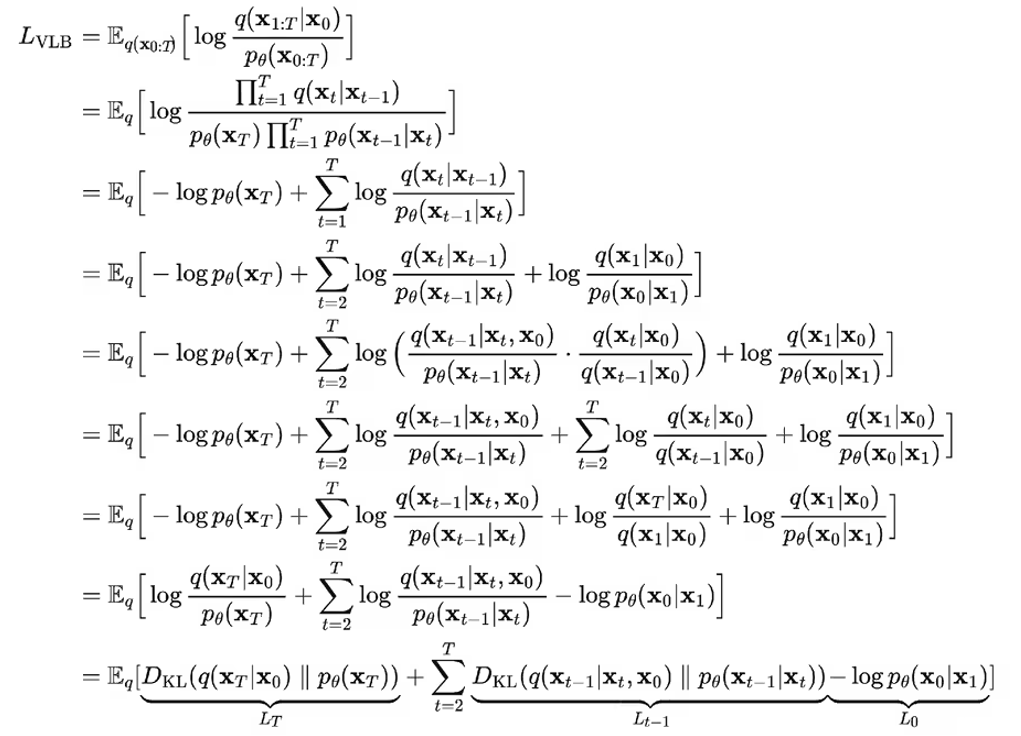
ELBO可以重写为：

\[L = L_T + \sum_{t>1} L_{t-1} + L_0\]

其中：

\(L_T = D_{KL}(q(x_T|x_0) \| p(x_T))\)
\(L_{t-1} = D_{KL}(q(x_{t-1}|x_t,x_0) \| p_\theta(x_{t-1}|x_t))\)
\(L_0 = -\log p_\theta(x_0|x_1)\)

作者发现使用简化的训练目标可以获得更好的样本质量：

\[L_{simple}(\theta) := \mathbb{E}_{t,x_0,\epsilon}\left[\|\epsilon - \epsilon_\theta(\sqrt{\bar{\alpha}_t}x_0 + \sqrt{1-\bar{\alpha}_t}\epsilon, t)\|^2\right]\]

# Algorithm 1: Training
while not converged:
    x_0 = sample_data()              # 采样原始图像
    t = sample_uniform(1, T)         # 采样时间步
    ε = sample_normal()              # 采样噪声
    loss = mse(ε, predict_noise(x_0, t, ε))  # 计算损失
    update_parameters()              # 更新模型参数

# Algorithm 2: Sampling
x_T = sample_normal()               # 从标准正态分布采样
for t in reversed(range(1, T+1)):
    z = 0 if t == 1 else sample_normal()  # 采样噪声
    # 预测并更新x_{t-1}
    x_prev = predict_mean(x_t, t) + σ_t * z
return x_0

采样算法详解

在DDPM中，完整的采样过程如下：

def sample(model, shape):
    # 从标准正态分布采样初始噪声
    x_T = torch.randn(shape)
    x_t = x_T

    # 反向去噪过程
    for t in reversed(range(1, T+1)):
        # 预测噪声
        epsilon = model(x_t, t)

        # 计算均值
        alpha_t = 1 - beta[t]
        alpha_bar_t = alpha_bar[t]

        # 计算均值和方差
        mean = (1 / math.sqrt(alpha_t)) * (x_t - (beta[t] / math.sqrt(1 - alpha_bar_t)) * epsilon)
        var = beta[t]

        # 添加采样噪声（在t=1时不添加噪声）
        z = torch.randn_like(x_t) if t > 1 else 0
        x_t_minus_1 = mean + math.sqrt(var) * z
        x_t = x_t_minus_1

    return x_0

关键步骤：

从标准正态分布采样初始状态\(x_T\)
逐步应用学习到的反向过程
通过预测噪声来计算均值和方差
采样下一个状态，直到生成\(x_0\)

DDPM的改进

加速采样

标准DDPM需要1000步采样，计算量大。改进方法包括：

DDIM (Denoising Diffusion Implicit Model)：通过确定性采样和跳跃步骤减少采样次数
预测器-校正器方法：结合ODE和SDE方法提高采样效率
知识蒸馏：训练更小的模型快速生成样本

条件生成

DDPM可以扩展为条件生成模型：

分类器引导采样：使用分类器梯度指导扩散过程
文本引导扩散：通过文本条件控制图像生成方向
结构驱动生成：通过结构信息（如分割图、草图）控制生成结果

总结

DDPM扩散概率模型的思想来源是非平衡热力学，通过逐步添加噪声来生成图像。前向过程是一个马尔科夫链，且通过重参数化等推导，使得可以直接用\(x_0\)对任意的时间步\(x_t\)进行采样。而反向过程也定义为一个马尔科夫链，用神经网络来拟合真实的后验分布，通过变分法得到优化目标，并通过重参数化来化简优化目标。DDPM的训练目标是最大化ELBO，并通过简化的训练目标来提高采样效率。但DDPM存在的限制为：要求过程为马尔科夫链，所以很缓慢，且无法处理非马尔科夫链的模型。

主要优势与其他生成模型的比较

样本质量高
训练稳定
实现简单
可解释性强

模型类型	优势	劣势
GAN	快速采样，高质量样本	训练不稳定，模式崩溃
VAE	易于训练，良好的表示	样本质量较低
自回归	高精度细节	采样慢，序列依赖
流模型	精确似然，可逆	架构受限，计算复杂
DDPM	高质量样本，稳定训练	采样慢，计算密集